Zero Knowledge
Basic Zero Knowledge
Definition: A proof system for membership in is an algorithm such that :
- Completeness: If , then , .
- Soundness: If , then .
Definition: A NP proof system for membership in is an algorithm such that :
- Completeness: If , then , .
- Soundness: If , then .
- Efficiency: halts after at most steps.
Definition: if there is a poly-time algorithm such that .

Definition [GMR'85]: An interactive proof system for is a algorithm and a function such that :
- Completeness: If , then .
- Soundness: If , then .
- Completeness and soundness can be bounded by any and as long as
- ,
- .
- independent repetitions .
- is a special case (c(|x|) = 1 and s(|x|) = 0).
- is a special case (no interaction).
Proposition: .
- NP proof for not self-evident.
- This suggests that maybe .
- Turns out that (in fact ).
Theorem [LFKN'90]:
Theorem [Shamir’90]:
Definition [GMR'85]: An interactive proof for is (honest-verifier) zero-knowledge if :
- We use to denote ’s view.
- Usually denotes 's output.
- Simulator for 's view implies simulator for 's output.
An interactive proof for is not (honest-verifier) zero-knowledge if :
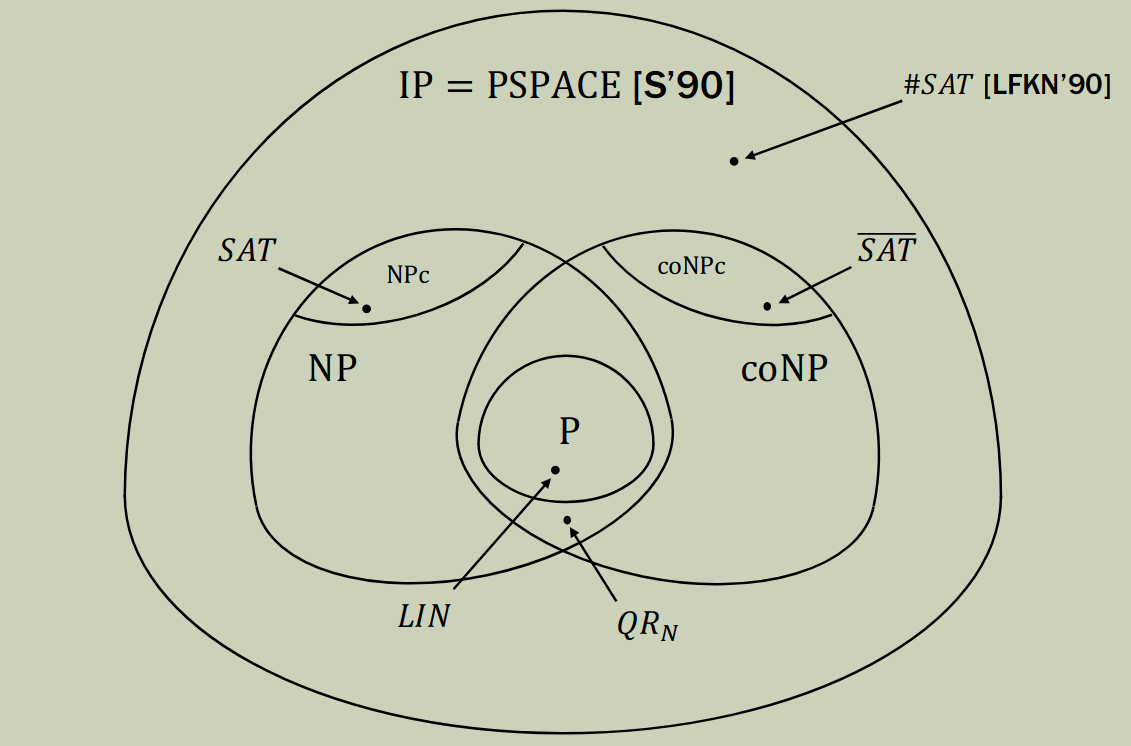
Proposition: .
Definition: An interactive proof for is prefect zero-knowledge if :
Proposition: .
- "black-box" ZK (stronger): :
- We allowed to run in expected polynomial time.

Definition: An interactive proof for is (perfect) zero-knowledge wrt auxiliary input if :
- captures "context" in which protocol is executed.
- Other protocol executions ("environment").
- A-priori information (in particular about ).
- Simulator is also given the auxiliary input .
- Simulator runs in time .
- Auxiliary input is essential for composition.
Theorem: ZK is closed under sequential composition.
Zero Knowledge and NP
Theorem [F'87, BHZ'87]: If then the polynomial-time hierarchy collapses to the second level.
Statistical ZK: (我猜有 wrt Auxiliary input):
Theorem [F'87, BHZ'87]: If then the polynomial-time hierarchy collapses to the second level.
Computational ZK: :
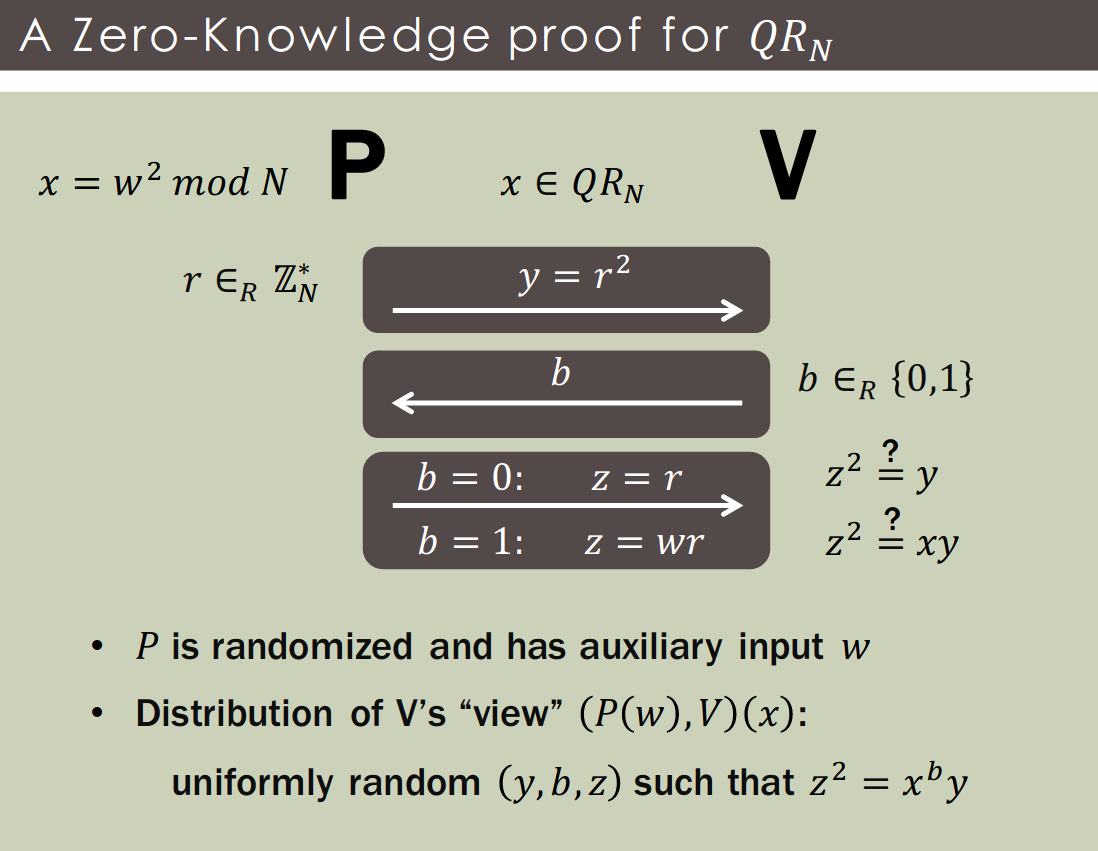
Theorem [GMW'86]: Suppose one-way functions exist. Then .
Theorem [GMW'86]: If statistically-binding commitments exist then .
Theorem [B'86]: If statistically-binding commitments exist then
Theorem [OW'90]: If proofs for languages outside of then there exist functions with one-way instances.
Theorem [OW'90]: If proofs for languages that are hard on average then there exist one-way functions.
.
Computational ZK: :
Zero-Knowledge Proof of Knowledge

A proof system has knowledge soundness with error if there exists a PPT s.t. for every prover , if convinces of with probability , then outputs s.t. with probability at least .
An Alternative Formulation:
Motivation: one can trade off running time and success probability
- Definition says: run in PPT and output w.p.
- Alternative definition: run in expected time and always output
A proof system has knowledge soundness with error if there exists a s.t.for every prover , if convinces of with probability , then outputs s.t. in expected time . 
A proof system is a zero‐knowledge proof of knowledge if it has
- Completeness: honest prover convinces honest verifier
- Zero knowledge: ensures verifier learns nothing
- Knowledge soundness: ensures prover knows witness
Zero knowledge is a property of the prover
- Prover behavior is guaranteed to reveal nothing
- Protect against a cheating verifier
Knowledge soundness is a property of the verifier
- Verifier behavior guarantees that prover knows witness
- Protect against a cheating prover


Strong Proofs of knowledge
A proof system has strong knowledge soundness if there exists a negligible function and a (strict) PPT s.t.for every prover , if convinces of with probability , then outputs s.t. with probability at least .
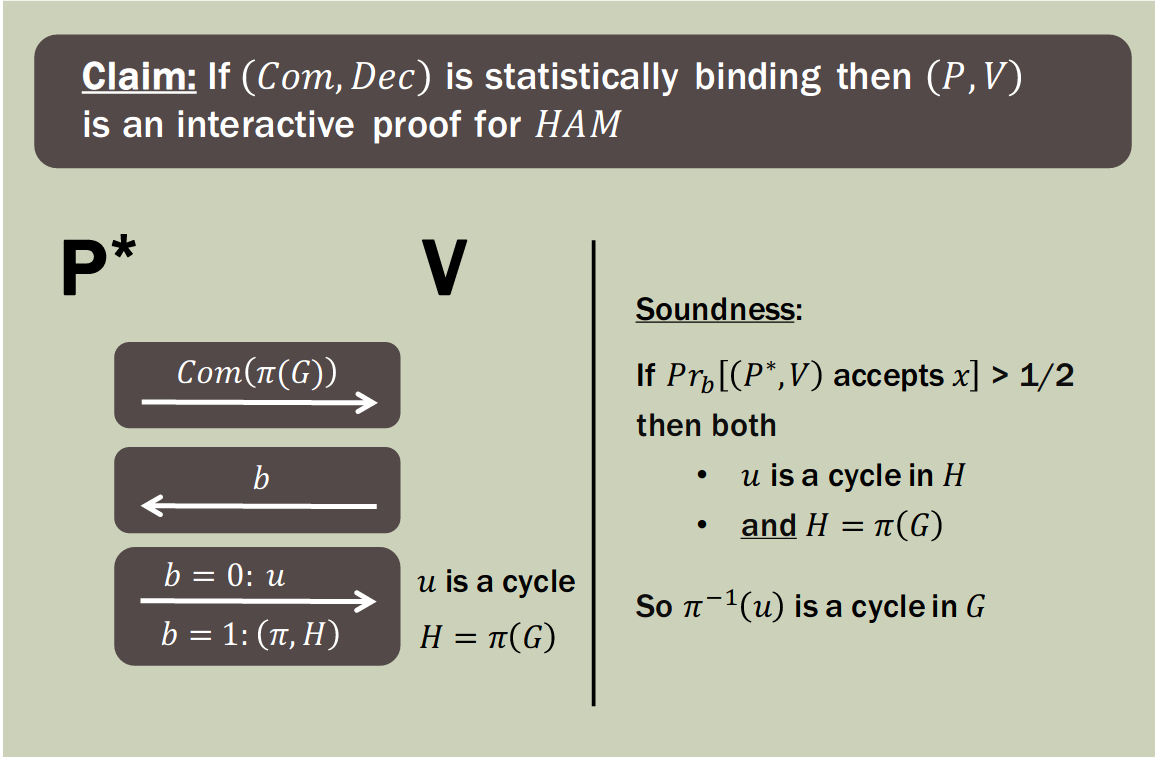
Theorem: sequential Hamiltonicityis a strong proof of knowledge.
We cannot construct constant round strong proofs of knowledge. (even for un black-box)
witness‐extended emulation
A witness‐extended emulator outputs a VIEW and some :
- The view output is indistinguishable from a real execution
- The probability that the view is accepting and yet is negligible
- runs in expected polynomial‐time
Lemma: If is a ZKPOK, then there exists a witness extended emulator for .
- Very useful when use ZKPOK inside proofs of security (and greatly simplifies)
- Can also formalize an ideal ZK functionality:
Lemma: If is a ZKPOK, then it securely computes the ideal ZK functionality (in the secure computation sense).

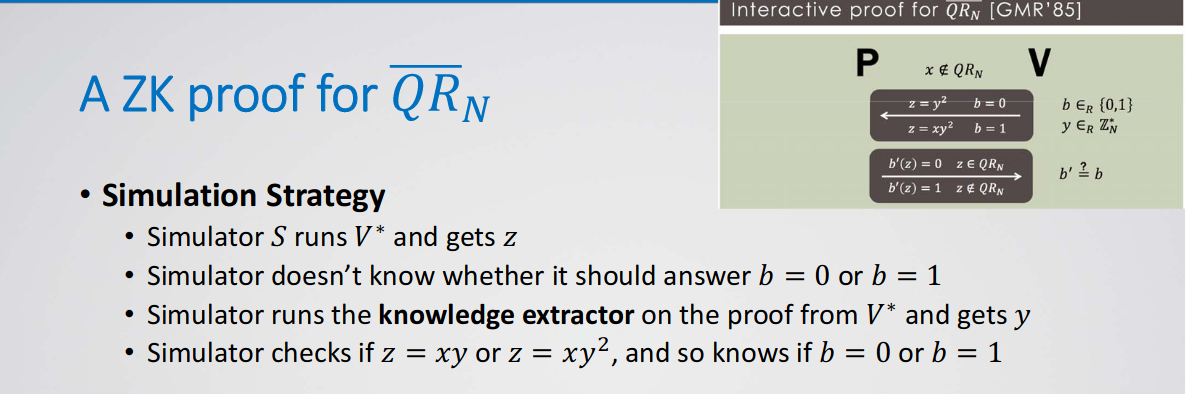
Constant-Round Zero-Knowledge Proofs

Definition: A statistically-hiding satisfies:
- Statistical hiding:
- Computational binding:


这里算的是期望,不abort,然后得到valid不停尝试的次数
Theorem [GK'91]: If statistically-hiding commitments exist then every has a ZK proof with soundness error .
Round-optimal[K'12]: if a language has a four-round zero-knowledge proof then


 Commitment from prover is statistically-binding. Commitment from verifier is statistically-hiding.
Commitment from prover is statistically-binding. Commitment from verifier is statistically-hiding.
Witness Indistinguishability and Constant-Round Arguments
Definition [BCC'86]:An interactive argument system for is a algorithm and a function such that :
- Completeness: If , then $\Pr[(P, V) \text{ accepts }x = 1
- Computational soundness: If , then PPT
- Computational soundness is typically based on a cryptographic assumption (e.g. CRH)
- Hardness of breaking the assumption is parametrized by security parameter
- Independent parallel repetitions do not necessarily reduce the soundness error [BIN'97]
CZK Proofs
- Soundness is unconditional (undisputable)
- Secrecy is computational - suitable when secrets are ephemeral and "environment" is not too powerful
SZK Arguments
- Secrecy is unconditional (everlasting)
- Soundness is computational – suitable when prover is a weak device and no much time for preprocessing
Theorem: If statistically-hiding commitments exist then there exists an SZK argument for .

Witness-indistinguishable:
Witness independent:
Defined with respect to some -relation .
Definition [FS'90]: is witness indistinguishable wrt if PPT ,
- Holds trivially (and hence no security guarantee) if there is a unique witness for
- Interesting (and useful) whenever more than one
- Holds even if are public and known
- Every ZKproof/argument is also WI
- WI is closed under parallel/concurrent composition

Definition: An interactive proof for is prefect zero-knowledge if :

Let denote parallel executions of
Theorem: If (P, V) is WI then (P^{(k)}, V^{(k)}) is also WI.

Theorem: Assuming non-interactive statistically-binding commitments, every has a 3-round witness-indistinguishable proof with soundness error
Theorem: Assuming 2-round statistically-hiding commitments, every has a 4-round witness-independent argument with soundness error
- The protocols are in fact proofs of knowledge
- We will use them to construct
- a 5-round SZK argument (of knowledge) for
- a constant-round identification scheme
- both with soundness error


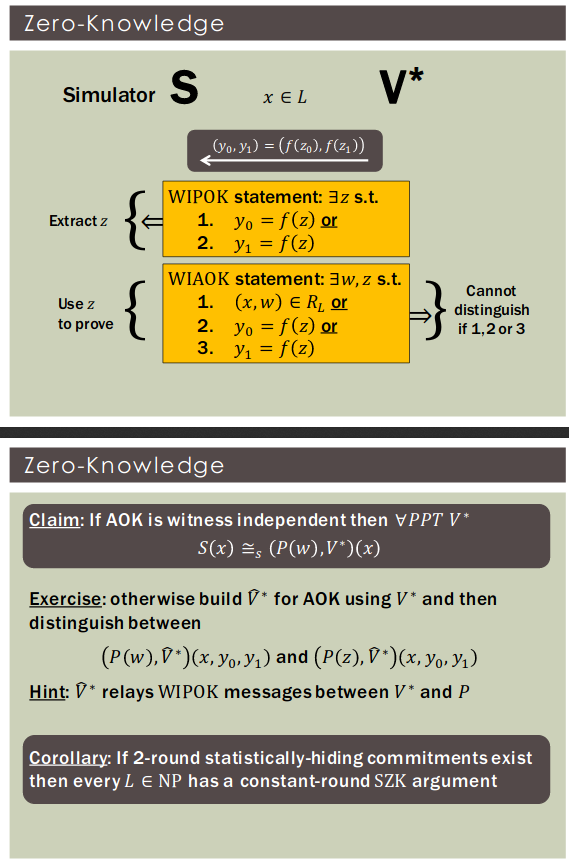
Corollary: If 2-round statistically-hiding commitments exist then every has a constant-round SZK argument.
In order to get 4-rounds ZK argument more ideas are required [FS'89, BJY'97]
Definition [FS'90]: is witness hiding with respect to , if PPT PPT
- WH is implied by ZK but does not necessarily imply ZK
- Defined with respect to an instance generator for
Claim: If an NP-statement has two independent witnesses then any WI protocol for is also WH

Non-Interactive Zero-Knowledge
Claim: If has a ZK proof in which prover sends a single message then .
Proof: Decision procedure for 𝐿:
- Given , run to get a simulated proof .
- Output .
- Completeness: If then simulated proof indis. from real proof accepts.
- Soundness: If then rejects all proofs (whp).
Non-Interactive Zero-Knowledge [BFM88]
- Key idea:trusted setup.
- Typically, the Common Reference String (CRS) model.
- A trusted party generates a CRS that all parties can see.
- Even Better: common uniform random string (CURS).
Definition: NIZK
- Completeness: if
- Soundness:if PPT , .
- Zero-Knowledge: “Can simulate view of the verifier”
- such that for
Variants of NIZKs
- Multi theorem:can-reuse CRS for many ’s.
- Adaptive soundness: sound even if chosen after CRS.
- Adaptive ZK: ZK distinguisher can choose after CRS.
- Statistical soundness (proof): sound against unbounded provers.
- Statistical ZK: ZK for unbounded distinguishers.
[FLS90]: NIZK for all of NP from Trapdoor Permutations*
Corollary: NIZK based on hardness of factoring.
Other known results:
- Bilinear maps [GOS06].
- Random oracle model.
- Obfuscation [SW13,BP15].
- Optimal hardness assumptions [CCRR18,CCHLRR18]
New & Exciting Feasibility Results [2019]
- LWE + circular security [CLW19]
- LWE! [PS19]
The FLS ParadigmConstruction has two main steps:
- Construct NIZK in the “hidden bits” model.
- Compile hidden bits NIZK to standard NIZK
The Fiat-Shamir Transform
The Fiat-Shamir Transform[FS86], Original goal was transforming ID schemes into signature schemes.
Theorem[PS96,Folklore]: for every constant-round interactive argument with negl. soundness, whp over , the protocol is secure. (Actually extends to some multi-round protocols.)
Claim: multi-round protocol with negl. soundness error s.t. is not sound (even in ROM).
Proof: Take any constant-round protocol with constant soundness and repeat sequentially.
Bad news [CHG98]: protocols secure in ROM but totally broken using any instantiation.
Do there exist hash functions for which the Fiat-Shamir transform is secure? Answer: we don’t (quite) know
Def: a hash family is FS-compatible for a if is “secure”.
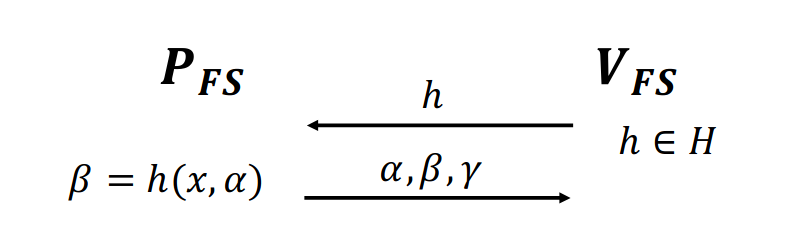
Def: is programmable if can sample random conditioned on .
Claim: if is programmable and is HVZK is ZK.
Proof: construct simulator.
- Sample .
- Sample conditioned on .
- Output .
Thm[B01,GK03]: protocols which are not FS-compatible for any .
[BDGJKLW13]: no blackbox reduction to a falsifiable assumption, even for proofs.
Lower Bounds and Limitations on Zero Knowledge
Unidirectional proof: a single message from to . Example: proofs
Theorem: Suppose that has a unidirectional ZK proof. Then
Theorem: Suppose that has a ZK proof in which the verifier is deterministic. Then
Theorem: Suppose that has an auxiliary-input ZK proof in which the prover is deterministic. Then .


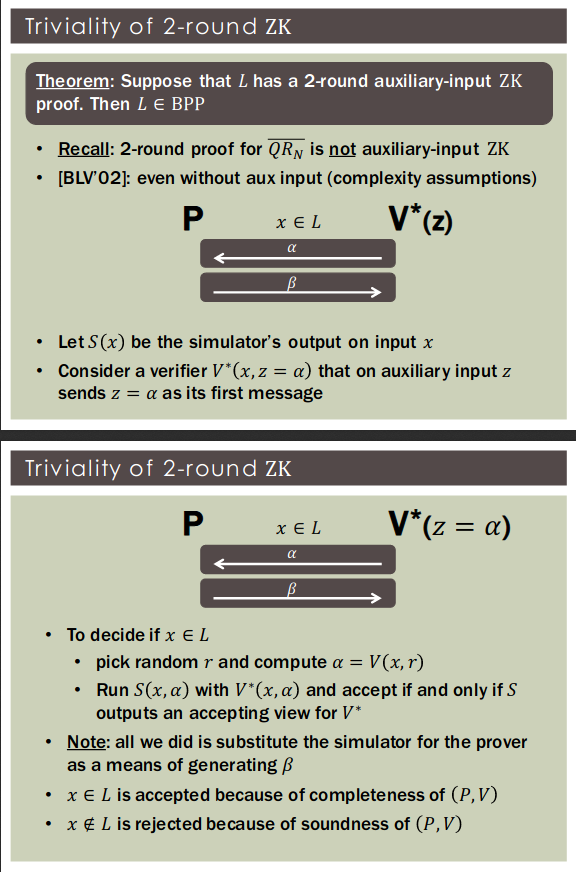
- Problem: ’s challenge is a string
- Simulator’s expected number of guessing attempts is
- Solution: Let verifier commit to in advance
- Yields 5 round proof (assuming OWF, 4-round argument)
original: black-box:
Triviality of BB ZK: only have (negligible error)
- constant-round public-coin BB ZKproofs/arguments
- 3-round BB ZKproofs/arguments
parallel repetition of and protocols are public-coin
applies to any constant number of rounds
if , even private coins do not help for BB ZK
Theorem[GK'91]: Suppose that has a constant-round, negligible error, public-coin ZKproof. Then .
Proof idea:
- Consider a PPT BB simulator
- Define a PPT that on input returns $m_i = f_K(m_1, \ldots, m_{i-1}),where is a pseudorandom function
- To decide if , run and accept if and only if the resulting transcript is accepting

Theorem[F'90]: There exists a ZK protocol that does not retain its ZK properties when run twice in parallel.
- There exist two provers such that each is ZK, but the prover that runs both in parallel yields knowledge
- Specifically, a cheating can extract a solution for a problem that is not solvable in polynomial time
- sends “knowledge” if and only if can solve a computationally hard challenge generated by
- Solutions are pseudorandom but can be verified by (which is unbounded)
- solves such pseudorandom challenges
- Both are ZK
- because a PPT is unable to solve the challenge and so will not send “knowledge”
- because the solution cannot be verified in poly time
- Can be made to work for poly time using statistically-binding commitments and ZKPOKs

Non Black-Box Zero Knowledge (Barak’s Protocol)
Goal: construct CZKargument
- with negligible soundness
- a constant number of rounds
- and public-coin
No has a black-box ZK protocol that is:
- constant-round
- negligible-soundness
- public-coin
So for must use a non-black box simulator
- On the one hand, should be easier than
- On the other hand, where do we even begin?
- Reverse engineering is difficult!
- Key insight: there is no need to reverse engineer
- Enough for to prove that he possesses 's code
Theorem [B'01]: If CRH exist, every has a constant-round, public-coin, negligible-soundness, ZK argument
- Idea: enable usage of verifier’s code as a “fake” witness
- In the real proof, the code is ’s random tape
- In simulation, the code is 's “next-message function”
- Since does not have access to 's random tape in real interactions, this will not harm soundness
- The simulator , on the other hand, will be always able to make verifier accept since it obtains ’s code as input
