Research

• Two-party private function evaluation
  • Introduction
  • My work
• Data trading for function evaluation result
  • Introduction
  • My work

Two-party private function evaluation

Introduction

The two-party private function evaluation (PFE) problem considers the scenario where a party $P_A$ holds a private function $f$ and (optionally) a private input $x_A$ while the other party $P_B$ has another private input $x_B$. These two parties intend to securely compute $f(x_A, x_B)$ without the existence of a third party. Finally, one or both parties may obtain $f(x_A, x_B)$, while they cannot deduce any other information beyond their specified outputs during the interaction. This task is accomplished just like there exists a trusted third party that receives inputs from two parties, computes $f(x_A, x_B)$, and sends it to one or both parties. Since both data and algorithms are valuable in numerous real-world scenarios, such as medical and commercial applications, it is very suitable to use PFE protocols in these scenarios. For instance, we consider the following business scenario between a traditional enterprise and an algorithm-driven company. The traditional enterprise has a dataset, while the algorithm-driven company holds a powerful data mining algorithm that can process this dataset. On the one hand, the algorithm-driven company does not intend to disclose the algorithm. On the other hand, since the dataset may contain sensitive data, the traditional enterprise is unwilling to reveal the dataset to others. We note that this dilemma can be solved by a PFE protocol that allows the traditional enterprise to receive the result of privately running the algorithm on the dataset.

My work

1. Making Private Function Evaluation Safer, Faster, and Simpler

   Yi Liu, Qi Wang, Siu-Ming Yiu

   To appear in Public-Key Cryptography. PKC 2022. [ePrintopen in new window]

   The main contributions of this paper are summarized as follows.

   • Active security. We provide the first constant-round actively secure PFE protocol with linear complexity in the two-party setting.
   • PVC security. We design the first constant-round PVC-secure PFE protocol with linear complexity in the two-party setting to gain much better efficiency.
   • Reusability (simplified follow-up executions). The global reusability property is added, i.e., one initiation for $f$ allows multiple executions for different inputs with different $P_B$.
   • Improvement We provide a significant improvement of protocol related to extended permutation.

2. Improved Zero-Knowledge Argument of Encrypted Extended Permutation

   Yi Liu, Qi Wang, Siu-Ming Yiu

   In Information Security and Cryptology. Inscrypt 2021. [ePrintopen in new window]

   Extended permutation (EP) is a generalized notion of the standard permutation, and it is useful for the problem of (PFE) to describe the topological structure of the circuit. We provide an improvement for the zero-knowledge argument of encrypted extended permutation protocol. We can instantiate our protocol to be non-interactive, while the previous protocol should be interactive. Meanwhile, compared with the previous protocol, our protocol is faster (e.g., more than $3.4\times$), and the communication cost is only around $24\%$ of the previous one.

Data trading for function evaluation result

Introduction

Data trading is an emerging business in which data sellers provide buyers with, for example, their private datasets and get paid from buyers. In many scenarios, sellers prefer to sell pieces of data, such as statistical results derived from the dataset, rather than the entire dataset. Meanwhile, buyers wish to hide the results they retrieve. We are wondering, in the absence of TTP, whether there exists a practical mechanism satisfying the following requirements: the seller Sarah receives the payment if and only if she obliviously returns the buyer Bob the correct evaluation result of a function delegated by Bob on her dataset, and Bob can only derive the result for which he pays. 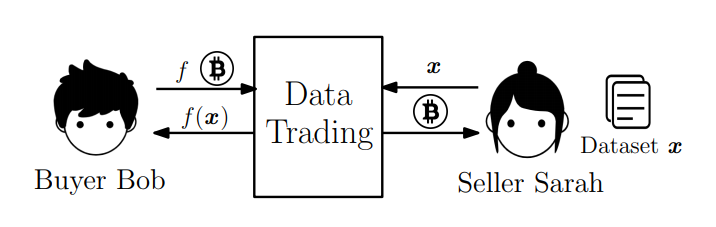Besides, we should ensure the consistency of datasets in two transactions, i.e., for each transaction (with the same buyer or with different buyers), Sarah should use the same dataset $\vec{x}$. In addition, because datasets during data trading tend to remain unchanged and consistent, we prefer a pre-processing procedure that amortizes the processing cost of datasets rather than a one-time solution. Here we call a solution one-time if every execution of such a solution involves a new entire processing procedure of the dataset.

The question is:

How to construct a practical mechanism for the requirements of data trading mentioned above, with the capability of supporting a wide variety of computing tasks?

My work

1. Blind Polynomial Evaluation and Data Trading

   Yi Liu, Qi Wang, Siu-Ming Yiu

   In Applied Cryptography and Network Security. ACNS 2021. [ePrintopen in new window]

   The main contributions of this work are in the following.

   1. Considering the scenario of data trading, we introduce a new cryptographic notion, namely, blind polynomial evaluation. We propose a generic construction of this notion using two compatible homomorphic encryption schemes.
   2. We propose a small-constant-round protocol to instantiate the generic construction to support polynomial evaluation over $\mathbb{Z}^*_n$. Furthermore, we extend our instantiation from polynomial evaluation over $\mathbb{Z}^*_n$ to that over $\mathbb{Z}_n$.
   3. We integrate our blind polynomial evaluation protocol with blockchain to support fair exchange in the data trading scenario.

2. An Improvement of Multi-Exponentiation with Encrypted Bases Argument: Smaller and Faster

   Yi Liu, Qi Wang, Siu-Ming Yiu

   In Information Security and Cryptology. Inscrypt 2020. [ePrintopen in new window]

   This paper provides an improvement for the multi-exponentiation with encrypted bases argument protocol. This protocol can speed up the encryption switching procedure used in the ACNS paper above.